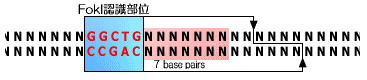DNAコンピュータ
イントロダクション計算機の歴史は私たちが思っている以上に古い。そろばんを計算機の歴史に入れるかどうかはともかくとして、おそらく現在の計算機の起源は、19世紀初等にC.バベッジの考え出した「差分機械(Difference Engine)」や「解析機械(Analytical Engine)」にまでさかのぼるだろう。もっとも、バベッジが構想したこれらの計算機は、結局製作されるまでには至らなかった。当時には、バベッジの考え出した精密な機械を製作できる技術がなかったためだ。 そして、20世紀を迎え、精密な工作機械類や真空管、トランジスタなど、信頼性が高くより能力の高い計算機が可能になった。とくにトランジスタが登場し、IC製造プロセスが確立されてからの約半世紀の計算機の進化は目覚ましい。現在のシリコンを基礎とするコンピュータは右肩上がりに成長し、その成長が 今後とまることを説得力をもって予言することはできない。 しかし、そんな今の計算機でも弱点がないわけではない。数学者の間でよく知られている「ハミルトン経路問題」や「充足可能性問題」と呼ばれる、しらみ潰しに答を探す必要のある問題では、逐次的な処理を行なう従来の計算機では、現実的な時間内に答えを見つけ出すことができない。 現在のコンピュータのそんな一面を補完することを期待して、現在研究が行なわれているのが、「量子コンピュ-タ」や「DNAコンピュータ」と呼ばれる、まったく新しいタイプのコンピュ-タだ。これらのコンピュータはともに新しい分野で、とても現在のコンピュータに対抗できるようなものではない。しかし、可能性としてはとても大きなものを秘めている。 今回は、そのDNAコンピュータの基本的性質や、最近の研究、そして展望などにスポットライトを当ててみることにしよう。 DNA基礎DNAコンピュータは生体、とくにDNAの複製の仕組みを真似ることに端を発している。そのためDNAコンピュータを理解するには、分子生物学の基本的 な知識が必要となる。このページでは、DNAコンピュータと関わりの深いものについて簡単に触れておく。 遺伝情報が親から子へと受け継がれていくためには、親とまったく同じDNAが合成される必要がある。この正確なDNAの複製には、たった4つの塩基対が 大きな役割を果たしている。アデニン(A)、グアニン(G)、チミン(T)、シトシン(C)の塩基対は、塩基対どうしの水素結合によって、AとT,CとG という選択的なペアを形成している。DNAが複製されるためには、いったんこの水素結合をたち切って、DNAの二重らせんをほどいてやる必要がある。いったん二重らせん構造がほどかれると、一本鎖のDNAはさまざまな酵素のはたすけをかりて巧みに複製を行なっていく。その様子は次のようなものだ。
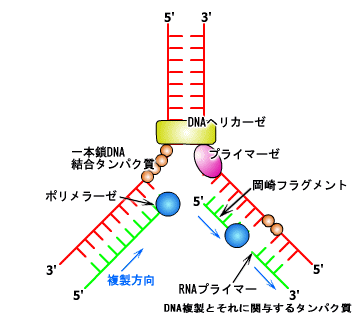
二重らせん構造をほどかれて一本鎖になったDNAに、「DNAポリメラーゼ」と呼ばれる酵素がとりつき、まるでレールの上を滑っていくかのように、重合を起こして鋳型となったDNAと相補的なDNAをあらたに合成する。ただし、DNAポリメラーゼが鋳型のDNAを進んでいく方向には決まりがあり、5’→3’方向へしか進むことができない。 ところが二重らせん構造をとっているDNAは、一方は5’→3’だが、もう片方は必ず3’→5’になっている。しかし、DNAポリメラーゼはこの方向に 伸長を触媒することはできない。そのためDNAポリメラーゼは、5’→3’のときのように連続的にではなく、図のように100~1000程度の短いDNA を不連続に新しいDNAを合成している。この断片的なDNAの構造を発見者にちなんで岡崎フラグメントと呼んでいる。この断片は「DNAリガーゼ」と呼ばれる酵素によって糊づけされるかのように連結されて長いDNA鎖になる。複製方向に一致する側に連続的に合成される娘鎖をリーディング鎖、複製方向に逆行し合成が不連続になる側の娘鎖をラギング鎖と呼んでいる。 実際のDNAの複製にはさらに多くの酵素やタンパク質が関与している。例えば、二重らせんをほどいて一本鎖をまっすぐにしているのは「DNAヘリカーゼ」だ。また、ラギング鎖でDNAポリメラーゼが合成を開始するきっかけをつくるのが、「プライマー」と呼ばれる、通常3~5個程度の塩基である。このプライマーを合成しているのが「プライマーゼ」と呼ばれる酵素である。 しかしその出力結果を得るとき、一つ一つのDNA分子だけで認識することは難しい。実際にはゲル電気泳動(下参考)などによって、特定のDNA分子の集団を認識しているので、同じ塩基配列を持ったDNAを大量に用意する必要がある。その方法が「ポリメラーゼ連鎖反応(PCR;Polymerase Chain Reaction)」と呼ばれる技術である。 具体的にPCRは次のような方法で行なわれる。
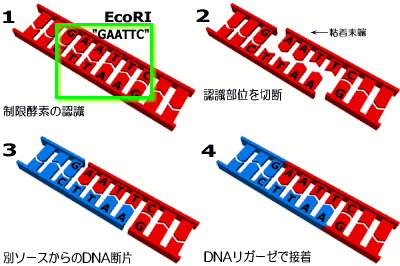
こうすることでn回のサイクルにより、理論上は目的のDNA鎖が2^n個(実際は2^n-2n,ただしnが大きいときには2^nと見なしてかまわない) できることになる。だいたい三時間ほどで20~50万倍ほどに増幅できる。現在PCRは実に多様な方面で重要な利用法が考え出されている。例えば、ウィル スや細菌の検出、遺伝子クローニング、遺伝子変異導入などがそうである。なお、はじめにPCRを考案したK.B.Mullisらは、この業績をたたえられ 1993年にノーベル化学賞を受けている。 複数種のDNA分子が混ざった溶液を寒天のようなゲル状の板の一端に置いて、板に電気を流す。すると、DNA分子は負の電荷をもっているので陰極へと移動するが、このとき分子量の小さいものは大きいものより速く移動する。したがって、DNAの分子量、つまり長さによって分離することができる。特殊な化合 物を使って紫外線を照射することで、DNAの移動後の様子が縞模様(バンド)としてみることができる。 「制限酵素(restriction enzyme)」は、DNA一本鎖上で特定の塩基配列を認識し、そのDNAを切断するという役割をもっている。制限酵素はDNAリガーゼとともに、60年代以降の組換えDNA技術で、非常に重要な位置を占めてきた。制限酵素で有名なものには、例えば"EcoRI"がある。
この酵素は、"GAATTC"という塩基配列を認識し、GとAの間で図のように切断する。すると、片割れのDNA断片の部分が生じるが、この箇所は水素結合で他のDNA断片と結合しやすいため、粘着末端(sticky end)と呼ばれている。この粘着末端を利用して、他の生物のDNAをDNAリガーゼを利用して接合することで組換えDNAができあがる。 この制限酵素EcoRIは大腸菌(Escherichia coli)から発見された酵素であるが、生体にとっての制限酵素のおもな役割は、バクテリアのような宿主組織をウィルスのような侵略者から守ることである。つまり侵略者のDNAを分解してしまうというものだ。ただし、このときに宿主組織のDNAも分解されてしまっては意味がないので、これを防ぐためにメ チラーゼと呼ばれる「修飾酵素(modifying enzyme)」で特定のヌクレオチドをメチル化して制限酵素がDNAにとりつけないようにしている。そのため修飾酵素は、よく制限酵素とペアとして考えられる。 DNAの分子演算 ここのページで紹介したいくつかのDNA関連の酵素は、DNAコンピューティングに必要な演算子としての性質をもっている。次のページ以降で具体的な方法について述べるが、ここで簡単にまとめておこう。これらの演算はDNAコンピューティングのほとんどのアルゴリズムにおいて基本的に共通している。
なお、すべてのDNAコンピューティングに共通しているとはいえないが、制限酵素などを使ったスプライシング(切断)演算も、複雑なDNAコンピューティングを実現するには重要である。これについては、「DNAコンピューティング/さまざまな酵素を使った複雑なDNAコンピュータ」で具体例を紹介している。 エイドルマンの発想DNAコンピュータの誕生 – DNAポリメラーゼとチューリング機械の類似性 今から50年ほど前にワトソンとクリックがDNAの二重らせん構造を提案した。DNAは巧みな二重らせん構造によって、生物にとって重要な情報の保存・複製を可能にしていることが分かった。しかもその情報密度は、DNA1gあたりでCD三兆枚分にも匹敵するほどだ。そのことを考えると、以前からDNA分子やその構造を利用してメモリなどに利用しようとする試みはあったに違いない。 ところが、DNA分子を演算装置として利用できることが実証されたのは1994年のことで、この実験は南カリフォルニア大学のエイドルマン(L.M.Adlemen)によって報告された[1]。これがDNAコンピュータのはじまりでもあるが、同時にその実験は分子コンピュータとしても初めてのものだとされている。 エイドルマンがDNAコンピュータを思いついたきっかけはなんだったのだろう?RSA公開鍵システムの開発者の一人でもあるエイドルマンは、もともとはコンピュータサイエンスを専門にしていた。しかし、93年ごろに、エイズに関する研究に参加する機会にめぐり合い、分子生物学の知識になった。そんな状況でエイドルマンが、ワトソンの分子生物学の教科書を読んでいたときに、「DNAポリメラーゼ(DNA polymerase)」の役割と、「チューリング機械(turing machine)」との間に類似性があることに気づいたのがDNAコンピュータ誕生のきっかけとなった。DNAポリメラーゼは、DNAの塩基配列を読み取 り、相補性的な塩基配列のDNAを複製する酵素である。一方、チューリング機械は、入力テープを読み取り、一定の計算処理を行なって出力テープを打ち出すというものだった。DNAポリメラーゼもチューリング機械も、「入力→処理→出力」という点では共通している。しかも、DNA鎖やテープを読み取るなどと いった物理的な役割も似ている。こうしてDNAポリメラーゼの役割にヒントを得たエイドルマンは、DNAコンピュータの製作にとりかかった。 DNAコンピュータの基本的な性格 DNAコンピュータは、シリコンを中心としたコンピュータとは仕組みが大きく異なっており、それによって得意不得意とする分野も違ってくる。 基本的に従来のコンピュータには、中心にマイクロプロセッサがひとつ存在しており、それが信じられなほどの速さで次から次へと計算処理をこなしている。一方でDNAコンピュータの場合は、分子一つ一つの処理速度は必ずしも高くないが、1度に何万、何億という分子が並列してさまざまな計算処理を行なうことが可能になる。そのためDNAコンピュータは、従来のコンピュータが苦手とする「ハミルトニアン経路問題」などが得意だと考えられている。これは計算処理の件数が指数関数的に増えていくという問題だ。DNAコンピュータといってもさまざまなタイプがあるが、並列処理が得意だという点ではほぼ共通しているだろう。 エイドルマンがDNAコンピュータの製作にとりかかったとき、DNAコンピュータに解かせた問題というのが、このハミルトニアン経路問題の一つである「セールスマン問題」だった。 エイドルマンがはじめて作ったDNAコンピュータ
まずはじめに、エイドルマンがDNAコンピュータの計算処理の対象とした、セールスマン問題がどのようなものか知っておいたほうがよいだろう。具体的には、次のような内容だ。 あるセールスマンが飛行機に乗って、セールスのために、いくつかの都市すべてを立ち寄らなければならないとする。ただし、このとき重要なのが、すべての都市どうしがエアラインで結ばれているわけでないということと、一度通った都市は二度と通ってはいけないという、2つの制限があるということだ。これが セールスマンの悩みの種となっている。 このフラッシュアニメーションの場合、「長崎」から出発して、「広島」、「大阪」、「東京」のすべての都市を一回ずつ立ち寄り、目的地である札幌に向かわなくてはならない。どのように旅行計画を立てることができるだろうか?この程度の問題なら簡単だろう。答えは「長崎>東京>広島>大阪>札幌」という順 になる。 この程度の数の都市とエアラインなら、紙や鉛筆を用意するまでもなく、頭の中で簡単に解けてしまう。しかし、都市の数が増えると、それを結ぶエアラインの数も急激に増えてくる。おそらく都市の数が10を越えるころには、頭の中では解けなくなり、コンピュータに頼ることになるだろ。しかし、今のコンピュータでも1万都市を超えるとなると、ハイパワーのものをいくつか同時に稼動させても数日はかかるだろう。いずれにしても、ハミルトニアン経路問題というの は、現在のコンピュータにとってはあまり相性のよい問題ではない。 この問題は数学的にもコンピュータサイエンス的にもよく出てくる古典的なものだ。では、エイドルマンはどのような方法で、これを解くことに成功したのだろうか?いくつかのステップに分けて考えてみよう。 [step1 考えられうるすべての旅行計画を手当たり次第つくる] 何はともあれ、コンピュータが「0/1」の文字に置き換えて処理しているように、DNAコンピュータもDNAの扱いやすい文字、つまり 「A,T,C,G」に置き換えてやる必要がある。そこで、5つの都市を区別できるように、次のように置き換えてやる。以下のようなDNA断片をつくる。
(※置き換え方にとくに決まりや法則性はないが、下で述べるエアラインと合わせて、お互いの都市が区別できればよい。) 次に、「長崎>広島」、「東京>大阪」など、それぞれのエアラインをDNAの文字に置き換えてやらなければならない。ここで、都市名とエアラインをうまく対応させる方法がないか考えてみよう。そこで「広島>大阪」の場合なら、「広島(ATGCCG)」の後半の3文字’CCG’と、「大阪(GCTACG)」の前半の3文字’GCT’をくっつけて’CCGGCT’を考え、これと相補性をもった’GGCCGA’を「広島>大阪」を表すエアラインとする。逆に「大阪>広島」なら’ACGATG’と相補性を持つもの、つまり’TGCTAC’となる。 この方法で置き換えれば、旅行経路を、都市の順番(「長崎」>「東京」>「広島」>「大阪」>「札幌」)に並べた’ATGCCGCTACGGTCGTACGCTACGCTAGTA’と、エアラインの順(「長崎>東京」、「東京>広島」、「広島>大阪」、「大阪>札幌」)に並べた’GGCGATGCCAGCATGCGATGCGAT’が、頭尾の3文字を除いて相補性を保っているという仕組みになっている。 あとは、都市とエアラインを表すDNA断片を試験管のなかに放り込むだけだ。そのときに小さなDNA断片を結合する「DNAリガーゼ」という酵素を一緒に入れておけば、小さなDNA断片は一本のDNA鎖になる。都市名を表すDNA断片とエアラインを表すDNA断片が、お互いにくっつき合って、答えとなる旅行計画書(目的のDNA断片)が自然とできあがるというわけだ。(DNAリガーゼについては、「DNAコンピュータ/DNAの構造と複製機能」を参照」) もちろんこれだけで、正しい旅行計画を表すDNA断片だけができるわけではない。むしろ正しい計画書はほんのわずかで、あとのDNA断片の集まりは数が足りなかったり配列が間違っていたりと、デタラメなものばかりができているはずだ。そのため、正しい旅行計画に相当するDNAだけを取り出してやる必要があるのだが、それはまるで大草原の中から小さな藁を拾い上げるようなもので、簡単なことではない。 それでは、どのような方法で、目的のDNA断片を拾い上げるのだろうか? [step2 デタラメな旅行計画書の山から、正しいものを取り出すには…]
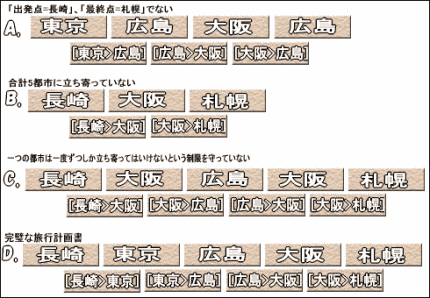
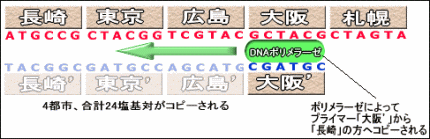
試験管の中には、さまざまの長さや配列のDNA断片が存在しているはずだ。そんな中でも、まずは出発点が「長崎」、最終地点が「札幌」になっているもの、つまりDNA断片の端が「長崎」と「札幌」を表す配列になっているものだけを拾い上げたい。これは、「ポリメラーゼ連鎖反応(PCR)」で「プライマー(primer)」という相補性を持ったDNA小断片を利用することで可能になる(ポリメラーゼ連鎖反応の大まかな仕組みを理解していないと、以下の文章が分かりにくいかもしれない。ポリメラーゼ連鎖反応については、「DNAの基礎知識/DNAの増幅 – ポリメラーゼ連鎖反応」を参照)。 1.今必要とされるDNA配列は出発点が「長崎(ATGCCG)」で最終地点が「札幌(CTAGTA)」のものだ。そこで、それと相補性をもったプライマー「長崎'(TACGGC)」と「札幌'(GATCAT)」を用意する。これによって、端に「長崎」と「札幌」をもつものばかりが複製される。 しかしこの時点では、「長崎」と「札幌」の間にくる都市の順序が間違っていたり、長すぎたり短すぎたりと、デタラメな旅行計画書が多く残っているはずだ。ただ、とにかくこれで出発地点が「長崎」、最終地点が「札幌」の計画書だけに絞り込むことができた。このとき図のAは取り除かれている。 2.次に、上で選択した計画書の中から、5つの都市だけを通っているものだけを選び出してみよう。ここでは、ゲルの上にDNA断片を染み込ませ両側から正負の電気をかけて、負に帯電したDNA断片を泳がせる「電気泳動」という操作を行う(電気泳動については、「DNAの基礎知識/電気泳動」を参照)。 このとき、DNA断片の長さ(重さ)に応じて、泳ぐ距離が変わってくるので、30塩基対(6塩基対×5都市)のものだけを選び出すことができるというわけだ。こうして図のBは取り除かれる。 これでだいぶ計画書を絞り込めたが、まだデタラメなものが含まれている。例えば「長崎>大阪>広島>大阪>札幌」(図のC)というような計画書が含まれているはずだ。つまり、すべての都市を1度だけずつ立ち寄るという条件を満たしていないものだ。そこで、今度はすべての都市に立ち寄っている計画書だけを選ぶために、次のような方法を考える。 3.たえば、東京(CTACGG)に立ち寄る計画書を拾い上げるために、東京と相補性をもった「東京'(GATGCC)」というDNA断片で、計画書のDNA断片を探す。このとき東京を含んでいない計画書があれば、それは「東京’」とうまくくっつかないので拾い上げられることはない。つまり、「長崎>大阪>広島>大阪>札幌」という間違った計画書はそのまま見捨てられてしまうというわけだ。こうして、5都市すべてに相補性をもったDNA断片で拾い上げの操作を行う。 この一連の結果得られるものは、出発は長崎、最終は札幌で、5つの都市すべてを5回だけで旅行するというもの・・・つまり、それこそが完璧な旅行計画書なのだ(図のD)。 [step3.完璧な旅行計画書の都市の順番を吟味する] さて、完璧な旅行計画書を選び出すことはできたが、実際に塩基配列を読んで都市がどのような順番で並んでいるかがわからなくては、旅行計画書を書いたことにはならない。現在では、直接DNAの塩基配列を読むことのできる特殊な顕微鏡(AFMなど)があるが、それらを使わない方法を考えてみよう。 ここではstep2のはじめに行ったプライマーを利用したポリメラーゼ連鎖反応(PCR)を行う。例えば、「大阪」の位置にプライマーを取り付けて PCRを行うとしよう。すると「長崎、…、大阪」のDNA断片ができる。それの塩基数を数えれば24塩基となるはずだ。したがって24÷6=4で大阪が4 番目ということになる。
あとは同じようにして、「東京」、「広島」とプライマーをつけてPCRを行えば、12,18塩基となり、2番目、3番目と判断することができる。 これでついに完璧な旅行計画を書き上げることができたわけだ。ついに出張セールスマンの悩みは解消された。 より大きな問題を解くには・・・ 94年にエイドルマンが行なった実験では、7都市14エアラインのセールスマン問題が対象となった。この実験はDNAコンピュータ、さらに分子コン ピュータの世界に大きな影響を与えた。しかしこの方法で、実用化を目指そうとするとき、大きな障害が姿をあらわす。 都市数を増やしていくこと、つまり、変数の多い複雑な問題を解くときに、物理的制約が大きな障害となってくるのだ。例えば、次のようなものが挙げられる。 1.操作ステップ数が増加する 実は、1に関しては、それほど致命的な問題ではないかもしれない。現在も発展を続けているバイオテクノロジーや半導体加工の技術を援用すれば、ほぼすべてのステップの操作を自動化することも不可能ではないだろう。 2のエラー率の問題は、重要なポイントである。基本的に、ステップを重ねることに誤差が蓄積して行くので、規模の大きな問題を解くときには、最終的な解がまったくデタラメなものになってしまうかもしれないからだ。 さらに厄介なのは3である。仮にエラー率の障害を克服できたとしても、それだけでは3の障害は解決しない。 従来のコンピュータではハミルトニアン経路問題などを解くには、変数の数に応じて指数関数的な時間が必要だった。一方、DNAコンピュータの方は、指数関数的に増える解の候補を表現するDNA分子をあらかじめ用意しておかなくてはならない。ということは、問題の大きさによっては、必要なDNA分子が地球の質量分というように非現実的な値となることがある。仮にそれだけの量のDNA分子を用意できれば、DNAコンピュータは並列的にその問題を解いてくれるだろうが、そのための準備をするのは現実的でないというわけだ。この解決には必要なDNA分子の数を減らせるようなアルゴリズムが必要となる。 ref. いろいろな酵素を使った複雑なDNAコンピュータエイドルマンの発想は、DNAコンピュータの実現の可能性を示すものだったが、94年にエイドルマンが提案した方法のままでは、実用的なDNAコンピュータを作るのが難しいことはわかっていた。例えばエイドルマンの実験では、正しい答えとなるもの以外にも多くのDNA断片ができてしまう。そのため、あらかじめ必要となるDNAの量は、問題が複雑になるにつれて急激に増えてしまう。また、間違った答えのDNA断片を取り除くための操作回数も同様に増える。このような煩雑な操作や複雑な処理を自動で行なってくれるようなナノマシーンをつくることはできないだろうか? 残念ながら、現在のナノテクノロジーの技術ではこういったナノマシーンを組みたてることはできない。しかし、身近なところにナノマシーンは存在している。生体内では、すでに何億年も前からナノマシーンは存在している。何千、何万種類と存在している酵素を利用すればよいのだ。エイドルマンの94年の報告 で使われていた酵素は、DNAリガーゼとDNAポリメラーゼだったが、なにも酵素はこれだけではない。
たとえば、ウィスコンシン・マディソン大学の研究チームでは、蛍光体といくつかの酵素を利用することで、エイドルマンの実験では煩雑だった正しい答えの読み出し作業を大幅に簡略化している。[1] 他にも、特定の塩基配列を認識しDNAを切断する「制限酵素」を利用して、複雑な計算処理を行なう実験も行なわれている。このページでは、この制限酵素をうまく使ったイスラエル(Weizmann Institute of Science)のE.Shapiroらの研究チームについて取り上げてみよう。[2] 一般に制限酵素というのは、例えば、EcoRIのように認識配列の部分を切断することが多い(「DNAコンピュータ/DNA基礎」)。しかしShapiroらの利用した制限酵素FokIは、認識配列からすこし離れた任意の塩基配列(9/13塩基目)を切断するという特殊なものだ。
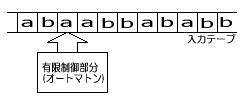
DNA分子による有限制御部分の設計 この研究チームが制限酵素を使った実験で題材にした数学的なモデルは、2つの内部状態(S0,S1)と2つの入力(a,b)をもつ有限オートマトン(finite automaton)だった。オートマトンというのは、もともとは自動人形という意味だったが、とくにコンピュータサイエンスの世界では、一定の手続きにしたがって情報をある形から別の形に変換する装置という意味で使われている。入力テープを挿入すると、オートマトンはテープにそって動きながらデータを読 み取り、一連の計算処理後にはその結果をテープに打ち出す。その模式図を下に示す。
一般に、2つの状態と2つの入力を持つ有限オートマトンには、以下の8つの遷移規則が存在している。そのため、遷移規則の選択の仕方は2^8-1=255通り存在している。また、最初に信号を受理できる状態は(S0,S1,S0/S1)の3つなので、その選択の仕方は3通り存在している。したがって、最大765(=255X3)通りのプログラムが書けることになる。
遷移規則表;2状態2信号のとき この765個のプログラムのなかで、面白そうな具体例を一つ取り上げてみよう。
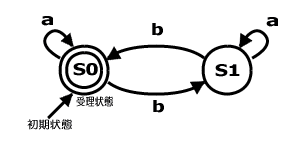
この図の場合では、bが偶数回でないと入力が受理されない(最終状態が受理状態S0にならない)。つまり、bの数の奇偶を判断できる。つまり、aba,aa,…といった入力は受理されず、abab,aabb,…といった入力が受理されるわけだ。 実際にこのような処理を行なうためには、プログラムの書き込まれた有限制御部分をDNA分子を使って組み立ててやる必要があるが、具体的にどのように行なったかは、以下のサイトなどを参考にしてほしい。 Biological Nanocomputers: Why and How? – Shapiro Team, Weizmann Institute 120mlの液体の入った試験管では、入力分子であるDNA断片が10^12個分だけ、並列して同一の計算を進行している。そのときの全体の1秒間あた りの遷移回数は10^9回程度で、計算の成功率は99.8%程度だったという。また、消費電力はほとんどないに等しい。 さらに、それぞれの入力分子の反応(計算処理)は独立して行なわれている個とを利用して、同一の試験管内で2つの異なるプログラムを同時に行なわせても、期待通りに2つの反応が並列して起こることが確認されている。この実験では、並列処理をはじめとして省スペース、省エネなどDNAコンピュータの将来 的な可能性を示すものとなっている。 ref.
[2]Benenson, Y. et al. "Programmable and autonomous computing machine made of biomolecules" Nature, 414, 430 – 434, (2001) DNAコンピュータの展望とリンク集DNAコンピュータの展望 DNAコンピュータをはじめとする新しいパラダイムの計算機の必要性を議論するのに、時間計算量の評価がよく題材に取り上げられる。 逐次的(sequence)な処理を行う従来のコンピュータでは、ハミルトニアン経路問題(HPP)や充足可能性問題、暗号解読などを処理するのは不可能ではないが、指数時間(exponential time)を要し、現実的でない。しかし、DNAコンピュータは、これらの問題を線形時間(linear time)で解くことを可能にできる。というのも、DNAコンピュータでは、プロセッサにあたる演算分子の個数はPCRなどで指数関数的に増加できるためである。 このようなDNAの並列性(parallel)は大きな魅力ではあるが、プロセッサの数が増えることは、エラー率の問題も重要になってくる。たとえば、エラー率が10-4のときは必要なDNA分子がグラム単位で済む処理も、エラー率が10-2になることで地球の質量の23倍にもなるという報告もある。 現時点で、さまざまな数学的考察から、DNAの将来性が議論されているが、それは楽観的とも悲観的ともいえる。実際に試算されているエラー率があまりにも理想的で、技術的な実現が難しすぎるかもしれない。一方、予期できないほど急速な発展を続けるバイオテクノロジーの分野から、驚くほどDNAコンピュータの信頼性の向上させられる技術が開発されるかもしれない。 あくまで一般的な議論になってしまうが、建設的なDNAコンピュータの将来像というのは、従来のコンピュータにとって変わるものではなく、重要な側面を補完するものだろうと考えられている。 ナノエレクトロニクスより 量子コンピュータ 外部リンク L.Adleman – South California ニュース 用語解説:DNAを使って“計算”する「DNAコンピューター」 – 日経BizTech(2003/1) |