メゾスコピックサイエンス
イントロダクションメゾスコピック系とは? 金(Au)を次々と半分に切り刻んで小さくしていった場合、それはいつまでも、私たちの知っている金のままでありつづけるだろうか?何やら間の抜けた質問だが、考えてみる価値があるだろう。 そもそも、切り刻めるほどたくさんの金を手にする機会はめったにないかもしれない。しかし、たとえ小さな金の粒であっても、それを原子の塊として考えれ ば、数えきれないほどたくさんの原子からなっていることも事実だ。金の原子量はだいたい200程度なので、1グラム程度の金には3×1021個ほどの原子がつめ込まれていることになる。 このように想像出来ないほど多くの原子からなっている金を、一、二度だけ半分に切り刻んでも、性質が変わることはない。ところが、この操作を際限なく繰 り返して、数十nm程度の長さになってくると、あまり馴染みのない量子的な性質が顔を出す。例えば、直径が10nmの金の導線では、コンダクタンスについてオームの法則は成り立たずに、コンダクタンスが飛び飛びの値をとったりする。 ところで、私たちのよく知っている金と、この馴染みない金との境目が、どのくらいのスケールにやってくるのだろうか? 実は、その数字は具体的にいえるものではない。そうではなくて、電子が結晶内で原子の散乱を受けずに進むことの出来る距離(平均自由行程)より、試料の サイズが小さいときに、そういった量子的な現象が現れてくるのだ。つまり境界線は、電子の平均自由行程と試料のサイズとの間で相対的なものになる。あえて 数字を挙げるなら、数百nmから数nm程度の領域といったところだろう。 こういった面白い現象が現れる領域を「メゾスコピック系」と呼び、現在のナノテクノロジー、ナノサイエンスとちょうど同じスケールにあたっている。メゾスコピックサイエンスは低温物理なども含めて幅広い分野で研究されているが、ここでは、エレクトロニクス分野と関係が深いものを中心に取り上げることにしよう。
量子サイズ効果
そこで電子を波として考えれば、規則正しい結晶構造を無限に繰り返している金属内に存在している電子は、一様に広がった波のように考えることが出来る。また電子のエネルギー準位は、連続的なバンド構造をとる。 ところが、金属が切り刻まれてどんとんと小さくなり電子の波長程度の大きさになると、電子のエネルギー準位が離散的になることが知られている。このこと は、両端を固定された弦が、もはや自由な振動形態をとることが出来なくなり、基本振動、2倍振動・・・と離散的な値しかとれなくなることに似ている。こう して離散的なエネルギー準位をもつようになった電子の影響で、その金属の比熱や帯磁性には、それまでになかったような性質が現れてくる。低温の金属微粒子 でこの離散的な影響に気づき、国内で草分け的な研究を行っていたのは、東大の久保亮五だといわれている。そのため、エネルギー準位の離散化にともなうこう いった変化を久保効果と呼ぶこともある。 量子効果と次元 – 量子井戸、量子細線、量子ドット
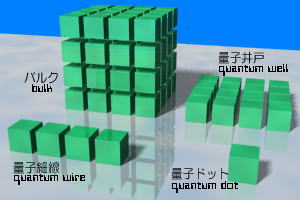
金属が電子の波長程度の大きさになって電子が閉じ込められることで量子サイズ効果が現れてくるが、閉じ込めの方位性によって次のように分けられる。 三次元方向に(電子からみれば)果てしなく広がった金属は「バルク(bulk)」などと呼ばれているが、これを一方向から狭めていき、その方向が電子の波長程度の大きさになると、電子は二次元的にしか移動できなくなる。これを「量子井戸(quantum well)」と呼んでいる。この量子井戸は超格子状にして、たとえば量子井戸レーザーなどのオプトエレクトロニクス機器に使われている。量子井戸のおかげで青色レーザーが可能になり、DVDや次世代光ディスクなどの大容量情報ストレージが実現した。(詳しくは「半導体レーザー」、「青色レーザーの実現までの道のり」などを参考に。) 二次元的に電子を閉じ込めたのが量子井戸だったが、さらにもう一つ別の方向を狭めていき、電子を一次元的に閉じ込めると、「量子細線(quantum wire)」となる。量子細線は、私たちの知っているバルクな導線と異なり、オームの法則に従わないなどの面白い性質が現れてくる。また、電子一つ一つを制御しながら送ることが出来る単一電子輸送などが期待されている。(これについてはあとで「単一電子輸送、クーロンブロッケイド」のページで取り扱う。) さらに別の方向を電子の波長程度の大きさにすると、もはや電子はどの方向にも進めなくなり、電子にとっては零次元の世界になってしまう。この状態が「量子ドット(quantum dot,量子箱とも)」と言い、現在光情報通信や量子暗号通信などの分野で研究が行われ、大きく期待されている。(詳しくは「量子ドット」で。) バリスティック伝導散乱されない電子の輸送
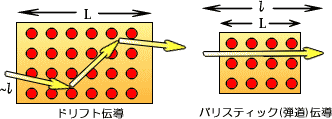
今ではトランジスタとエレクトロニクスは切っても切れない関係にあるが、エレクトロニクスの歴史が始まった頃は、トランジスタよりも真空管の方が中心的な 存在だった。真空管の基本的な原理は、真空中でフィラメントを加熱して熱電子を放出させ、それを電場でコントロールすることでいろいろな機能を実現すると いうものだ。つまり真空中で散乱されずに進む電子の振る舞いによって、いろいろな機能が実現されているのだ。 ところが真空管は、消費電力が大きい上に小型化が難しく、信頼性にも欠けることから、じきにバーディーン、ブラッテン、ショックレーらによって発明されたトランジスタに取って代わられることになった。(詳しくは「トランジスタ」で。) トランジスタに使われているのは半導体で、その性質を決めているのは、結晶中で自由に振舞う伝導電子である。伝導電子は結晶中の不純物などにぶつかって 散乱されながら進み、巨視的な現象としては私たちのよく知っているオームの法則として現れてくる。 G=σS/L :オームの法則 ところが現在の半導体デバイスは微細加工に次ぐ微細加工のおかげで、トランジスタはますます小さくなっている。そして電子が散乱される前に結晶内を通りすぎる、つまり電子の平均自由行程よりも結晶の方が小さくなるように加工することも技術的に可能になってきた。 これを可能にする方法は2つあり、電子の平均自由行程を大きくするか、それとも試料を小さくすればよい。前者については、試料を低温にするか、分子線エ ピタキシー(MBE)などの技術で高純度な結晶を生成することで実現できるが、現実的なエレクトロニクス応用を考えるなら室温での実現を期待したい。後者 については、電子線リソグラフィーなどで数十nm以下の微細加工が可能である。 G=2e^2/h: ランダウアーの公式、バリスティック伝導を表現する このように電子が散乱されずに結晶内を通り過ぎる現象を「バリスティック伝導(ballistic,弾道)」と呼ぶ。バリスティック伝導は特別な材料に限られた性質ではなく、ごく身近にある金属から有機分子まで幅広い材料で実現できるとされている。最近では、カーボンナノチューブがバリスティック伝導を示すことも分かっている。 バリスティックな伝導性を示す材料を電界効果(型)トランジスタ(FET)のチャンネルに用いれば、電子はソースからドレインまで散乱されることなく進み、スイッチング速度の速いトランジスタが実現できる。 なお、バリスティック伝導は電子が散乱されることなく進むことが出来るということから、超伝導のように電気抵抗がゼロかと思えるかもしれない。しかし実 際は、バリスティック伝導性材料を外部の試料と接続するときに、有限の電気抵抗が生じることが分かっている。そこで、バリスティック導電性の細線に有機分 子が付着すると、その電子散乱により電気抵抗が生じることから、分子レベルでの高感度センサーに応用しようという研究も行われている。 クーロンブロッケイド、単一電子トンネリング
メゾスコピック系で顕著にあらわれる電子の孤独癖 – クーロンブロッケイド 電子と電子が近づくとお互いに反発し合い斥力を生み出すが、例えば試料AからBへ電子が移動すると、Bには Ec=2e2/C のエネルギーが蓄えられることが知られている。しかしこの程度のエネルギー変化は、室温(300K程度)でバルクスケールの試料のもっている熱エネル ギーに比べればはるかに小さなものだ。電子一つがもぐり込んだことによるエネルギー変化は、この熱のゆらぎに対して十分無視できる。仮に1K程度の低温で も、原子がアボガドロ数個(1023)もあるバルクスケールなら、電子移動によるエネルギー変化は同じように無視できるだろう。 つまり、電子と電子が十分離れて存在できるバルクスケールでは、お互いに反発し合う孤独癖がほとんどあらわれてこないというわけだ。 ところがメゾスコピック系では話がまったく違ってくる。メゾスコピック系の試料では、その電気容量Cが極端に小さくなり、電子移動によるエネルギー変化Ecはもはや無視できないほど大きくなる。 バルクスケールではお互いに離れていたために孤独癖をほとんど見せなかった電子が、ナノスケールの狭い領域に押し込められたために反発力が大きくなり、孤独癖が顕著にあらわれるようになったと考えることも出来るだろう。 こうなるとナノスケールの試料AからBへ電子が移動することで生じる影響が非常に大きなものとなり、反発力によって電子の移動がブロックされるという現象がおこる。この現象のことを「クーロンブロッケイド(Coulomb Blockade)」と呼んでいる。 電子を一つ一つ制御するトランジスタ では、このクーロンブロッケイドという現象を、エレクトロニクス分野でどのようにいかすことが出来るだろうか?その代表的なものに「単一電子トランジスタ(SET,Single Electron Transistor)」がある。SETの原理は、基本的にはMOSトランジスタと同じであるが、ソースとドレインの間にトンネル障壁と呼ばれる絶縁層が 存在している。またトンネル障壁の間には、ナノスケールの量子ドット(電荷島ともいう)が存在している。(図1) このドットにソースから電子が一つ輸送されてくると、すでにドットの中にある電子の反発を受けてブロックされてしまう。そのためこのトランジスタ内に電 子を移動させるためには、ドットと静電結合したゲート電極に印可することでコントロールしてやる必要がある。 ゲート電極に正の電圧をかけると、ドット内のエネルギー準位が動き、ドットに入射した電子のエネルギーが離散エネルギーに等しいときにだけ電流が流れる。このような電流の流れ方をクーロンブロッケイド振動と呼んでいる。(図2,3) クーロンブロッケイドには電子の波動としての性質を示すトンネル効果が関わっているにもかかわらず、電子を一つずつ輸送するといった粒子性も同時に現れており、実に興味深い現象だといえる。 この現象によって電子を一つ一つ制御しながら輸送することが出来ることから、単一電子トランジスタという名前がついている。量子ドットのサイズがナノスケールに出来れば、このトランジスタは室温でも駆動することが実証されている。 このSETの利点は、電子数個でスイッチングを行っていることによる低消費電力の実現や、MOSトランジスタ特性と異なる点を生かした回路設計などがある。 リンク集ナノエレクトロニクスより |
|||||||||||||||||||