■論理ゲート
− 論理ゲートの基本、NOTゲート
論理ゲートの基本
論理回路の中で最も基本的な機能を持った回路であるのが「基本論理ゲート」である。そのなかでも特にベーシックな論理演算機能は以下の三つである。
1.「…でない」を意味する「否定論理(NOT)」
2.「…かつ…」を意味する「論理積(AND)」
3.「…または…」を意味する「論理和(OR)」
信じにくいことかもしれないが、この三つの組み合わせにより、どんなに複雑な理論でも実現することができることが数学的に証明されている。これから数ページで紹介する基本的な論理ゲートは簡単で退屈なものが多いかもしれないが、このいくつかを理解していれば、コンピュータの演算や判断、記憶の仕組みについて理解するのが簡単になる。
NOTゲート
まずは、最も簡単な「NOTゲート」についてみていこう。NOTゲート回路を組み立てるにはいくつかのパターンがあるが、ここではCMOSを使って組み立てたものについて考えていく。今後登場してくる基本的な論理ゲート回路もCMOSで組み立てたものを紹介する。(CMOS型トランジスタについては「トランジスタ/CMOSの仕組み」を参照。)
NOTゲートは入力(0/1の論理値)に対し、反転して出力する論理ゲートである。そのことから「インバータ」と呼ばれることも多い。下にNOTゲートの論理式(A)、真理値表(B)、論理記号(C)を示してある。
(A)論理式
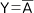
(B)真理値表
(C)論理記号

※1.「論理式」とは、記号化された命題間の論理的関係を、論理演算子( ̄,・,+)を用いて式の形で表したもの。入出力の関係で見た場合、右辺が入力記号に論理演算を施したもの、左辺が出力記号にあたり、両者を"="で結んでいる。
※2.「真理値表」とは、入力のとりうるすべての論理値に対して、出力の論理値の形で1対1に対応させたもの。
※3.「論理記号」とは、論理演算の操作を記号化したもので、実際の回路設計ではこの記号を用いて回路が表現されている。
CMOS型NOTゲートの回路構成例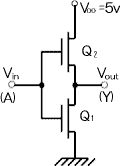
左にCMOS型回路で表したNOT論理ゲートの図が示してある。Q1はNチャンネルMOSトランジスタ、Q2はPチャンネルMOSトランジスタ。入力Aが「ハイ」つまり「1」のとき、Q1はON、Q2はOFFとなるので、出力YはQ1によりグラウンド(0V)に引かれて「0」となる。一方、Aが「ロウ」つまり「0」のとき、Q1はOFF、Q2はONとなるので、出力YはQ2より電源に引かれて「ハイ」すなわち「1」となる。
今後紹介する論理ゲートは、このCMOSインバータの回路構成が基本となっているのでしっかりとおさえておこう。
|
|