■論理ゲート
− 基本論理ゲートから回路を組み立てる:比較回路と一致回路
退屈な基本論理ゲートについての説明を一通り終えると、これらを組み合わせて限りない種類の論理回路を組み立てることができる。もちろんすべての論理回路について、ここで触れることはできないので、簡単で基本的な回路を触れるだけにしよう。まずは、複数の入力信号の大小を比較し、その結果を出力する機能を持った回路である「比較回路(comparator)」について見てみることにしよう。比較回路は二つ以上の多入力だが、今回は最も簡単な「2入力・3出力」について扱う。
・比較回路
下に比較回路の論理式、真理値表、論理記号についてそれぞれ示した。3出力のX、Y、Zは、それぞれ"A>B"、"A=B"、"A<B"としている。つまりX、Y、Zのどれが「1」になるかで、A、Bの大小関係が表される仕組みになっている。
(A)論理式
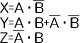
(B)真理値表
| 入力 |
出力 |
| A |
B |
X |
Y |
Z |
| 0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
(C)論理記号
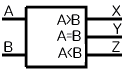
比較回路は様々な方法でつくることができるが、ここではNOT、AND、ORゲートを使って組み立てた例を示す。それぞれのゲートの接点に、論理式の途中結果が示してあるので、それを追っていけば比較回路が機能していることがわかるだろう。
・一致回路
次に、入力信号の論理値の一致・不一致に関する論理的判断を行う「一致回路」を紹介する。この場合、出力Yの意味について、次のように定めている。
A=B(A=B=「1」または「0」)のとき、Y=「1」
A≠B(A=「1」かつB=「0」またはA=「0」かつB=「1」)のとき、Y=「0」
(A)論理式

(B)真理値表
| 入力 |
出力 |
| A |
B |
X |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
(C)論理記号
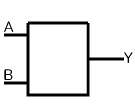
平たく言えば、出力Yが「1」なら一致で、「0」なら不一致と言うことになる。下に一致回路の構成例を図に示した。
|
|