■論理ゲート
− 基本論理ゲートから回路を組み立てる2:加算器
加算器(adder、アダ−)とは、足し算の機能を持った演算器のことである。複雑に組み合わせていけば十進法も可能だが、ここでいう足し算とは二進法のものが基礎となっている。加算器には、下位からの桁上げを考慮しない「半加算器」と、下位からの桁上げも考慮する「全加算器」の二種類がある。全加算器は半加算器を組み合わせることでつくることが可能だ。以下でこの二種類の加算器について具体的に見てみよう。
・半加算器(HA;Half Adder、ハーフアダ−)
加算器のうち、下位の桁からの桁上げ(「キャリー(carry)」)を考慮しないものを半加算器と呼んでいる。半加算器は2入力A,Bに対し、AとBの和「S」(Sum)とキャリー「C」の二つを出力する。下に半加算器の論理式、真理値表、論理記号を示す。
(A)論理式
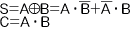
(B)真理値表
| 入力 |
出力 |
| A |
B |
S |
C |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
(C)論理記号

半加算器の回路を実際に組みたてるには様々な方法があるが、ここではNOT、NANDゲートによる構成例を示す。論理記号の接点部分に論理式の途中結果が示してあるので、実際に上の真理値表のようになるか確かめてみてほしい。また論理式の変形には「ド・モルガンの定理」を利用している。
・全加算器(FA;Full Adder、フルアダー)
全加算器は本来の2入力A,Bだけではなく、下位の桁からのキャリーCも入力して加算し、和Sと次の桁へのキャリーC+を出力する。下に全加算器の論理式、真理値表、論理記号、構成回路例を示す。
(A)論理式
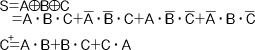
(B)真理値表
| 入力 |
キャリー
C |
出力 |
| A |
B |
S |
C+ |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
(C)論理記号

全加算器の構成回路例
|
|