■論理ゲート
− AND、OR、NAND、NORゲート
・ANDゲート
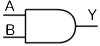
論理積(AND)は「AかつB,Aであり同時にBである」を意味し、このような論理演算機能を持った回路が「ANDゲート」である。具体的には、入力信号がすべて「1」のときだけ出力Yが「1」となり、他の場合はすべて出力が「0」になるというものだ。ANDゲートには2個以上の多入力ゲートがあるが、ここでは「2入力・1出力」の場合を考える。下にANDゲートの論理式(A)、真理値表(B)、論理記号(C)を示す。
(A)論理式

(B)真理値表
| 入力 |
出力 |
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
(C)論理記号
また、ANDゲート回路について、CMOSを使った構成例を紹介しておこう。この図の場合では、全体出力Yの他に、最終段のインバータに対する入力Y'を考えると理解しやすい。
例えば、入力A、Bがともに「1」ならば、Y'はNMOS型トランジスタQ1、Q2を介してグラウンドに引かれる。そのためY'は「0」となる。次に最終段のインバータに注目して、前段の入力Y'が「0」なので、全体の出力Yは「1」となる。これ以外の入力の場合は、Q3またはQ4を介してY'が電源に引かれ「1」となるので、全体の出力は「0」である。
・ORゲート
論理和(OR)は「AまたはB、AであるかあるいはB」を意味し、このような論理演算機能をもった回路が「ORゲート」である。具体的には、入力信号がすべて「0」のときだけ出力Yが「0」となり、それ以外の場合はすべて出力が「1」になる。下にORゲートの論理式(A)、真理値表(B)、論理記号(C)を示す。
(A)論理式
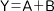
(B)真理値表
| 入力 |
出力 |
| A |
B |
Y |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
(C)論理記号
ORゲート回路について、CMOSを使った構成例を紹介しておこう。この図の場合でも、全体出力Yの他に、最終段のインバータに対する入力Y'を考えると理解しやすい。
例えば、入力A、Bがともに「0」ならば、Y'はPMOS型トランジスタQ3、Q4を介して電源に引かれる。そのためY'は「1」となり、全体の出力Yは「0」となる。これ以外の入力の場合は、Q1またはQ2を介してY'がグラウンドに引かれるため、Y'は「0」となり、Yは「1」となる。
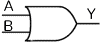
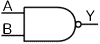
・NANDゲート
NANDとは、論理積(AND)の否定(反転)のことで、NAND=NOT(AND)とあらわすことができる。下にNANDゲートの論理式(A)、真理値表(B)、論理記号(C)を示す。論理式については、「ド・モルガンの定理」から、出力Yを入力A、Bの否定 、 、 の和と表すこともできる。 の和と表すこともできる。
なお、NANDゲート回路をCMOSを使った組み立てた場合、先ほどのANDゲート回路で最終段のインバータを取り除いた簡単なかたち(つまりY'が全体出力Y)になる。NANDゲート回路がANDゲート回路より簡単に構成できるのは、CMOS回路ではNOTゲートが基本となっているためである。これは次に紹介するNORゲート回路でも当てはまることである。
(A)論理式
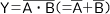
(B)真理値表
| 入力 |
出力 |
| A |
B |
Y |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
(C)論理記号
・NORゲート
NORとは論理和(OR)の否定(反転)のことで、NOR=NOT(OR)とあらわすことができる。下にNORゲートの論理式(A)、真理値表(B)、論理記号(C)をしめす。
(A)論理式
_______ __ __
Y = A + B (=A * B)
(B)真理値表
| 入力 |
出力 |
| A |
B |
Y |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
(C)論理記号

この他にも、XAND、XORゲートなどがよく使われる。
|
|