■量子コンピュータ
- Shorの因数分解アルゴリズム、他
背景
かつて暗号というのは、軍事目的など、ごく限られた範囲でのみ利用されていた。ところが現在では、インターネット上の商取引や重要文書のやり取りなど(意識するかどうかは別として)、暗号は日常的に利用されるようになってきた。しかし、インターネットでは不特定多数の利用者が集まってくるために、従来のような暗号ではいろいろと都合が悪い。そこで登場したのが、「公開鍵暗号」という画期的なアイディアだった。
この公開鍵暗号の代表的なものに「RSA」暗号(RSAは開発者R.Rivest,A.Shamir,L.Adlemanの名前からとっている)というものがある。
このRSAのアルゴリズムは因数分解を基礎にしている。この原理を理解するために、次のクイズを考えてみよう。
次の値の素因数分解を行なえ。
119423158423 = ? x
? (ヒント;2つの素数に分解できる)
ちゃんと因数分解はできただろうか?少なくとも紙と鉛筆だけで解くのは不可能だろう。では、こうしたら、どうだろうか?
次の計算を行なえ。
398477 x 299699 = ?
もう、何をいおうとしているのかお分かりだろう。つまり、
398477 x 299699 = 119423158423
について、左から右を計算することは簡単なのに、右から左を計算することは非常に難しいということだ(もちろん原理的にはとくことができるが、現実的な時間内にとくことが出来ない)。RSAは、因数分解のこの一方通行な性質を、上図に示すような暗号システムに対応させているのだ。
大きな値(例えば50桁)の因数分解は、現在のコンピュータにも苦手な問題といえる。公開鍵暗号というのは、コンピュータが現実的な時間内に大きな値の因数分解をとくことが出来ないということを安全性の根拠にしているのだ。
ところが、最も重要な暗号システムの一つであるRSAも、量子コンピュータの登場により、まったく無意味なものとなってしまう可能性があるのだ。量子力学的な「重ね合わせ」を利用することで、従来のコンピュータが宇宙の歴史ほどの時間をかけても解けなかったような因数分解を、量子コンピュータは数分、もしくは数秒で解いてしまうかもしれないのだ。この方法を具体的に示したのが、「Shorの因数分解アルゴリズム」である。このアルゴリズムは、量子コンピュータのキラーアプリとして、それまで学術的な範疇にとどまっていた量子コンピュータを社会全体の関心事にしてしまったのだ。
なぜShorのアルゴリズムか?
さて、いざコンピュータに整数Nの因数分解をさせようとするとき、どのようなプログラムを考えればよいだろうか?
まず誰でも思いつくのが、2,3,5....と2から(N-1)までの範囲にある素数を手当たり次第に探す方法だろうが、そのためにはあらかじめ(N-1)までの素数表を入手していなければならない。しかし素数表といっても、RSAの因数分解は素数表を利用して簡単に解けるようなものではない。とにかく、この方法では量子コンピュータの利点をいかしきれない。
そこでShorが利用した因数分解の方法は、以前からよく知られていた次のようなものだった。これは剰余が一定の周期で繰り返すという周期関数を利用したものだ。(ここからやや数学的な予備知識が必要となるが、ページの下のほうで補足している。)
1.Nより小さいxを適当に選ぶ。
2.xとNの最大公約数fを計算する。f=gcd(x,N) [補足1]
もしf≠1のときは、そのfがNの素因数である。(ここで操作終わり)
Compute f=gcd(x,N); if f≠1, return f. (It's
a factor.)
3.xrをNで割ったとき、その余りが1となる最小の整数rを探す。[補足2]
Find the least r such that xrmodN = 1
4.(xr/2-1)とNの最大公約数、もしくは(xr/2+1)とNの最大公約数のいずれかが1以外の数字なら、それがNの素因数である。
If either gcd(xr/2-1, N) or gcd(xr/2+1,N) is not 1, return it, it's a factor.
5.ここまでで素因数が見つからなければ、1に戻って操作を繰り返す。 |
このような方法で因数が求められるのは、周期関数の特徴のためである([補足1]を参照)。また、最大公約数を求めるのは、ユークリッドの互助法を使えば、短い時間で簡単に解ける。
はじめてこのアルゴリズムを見た人には、なかなかピンとこないかもしれない。そこで、15の因数分解を例に考えてみよう。
1'. N=15より小さい数を適当に選ぶ。ここではx=11を選んだことにする。
2'. 11と15の最大公約数は1である。したがって、次のステップへ進む。
3'. r=1のとき、111÷15=0...11
r=2のとき、112÷15=8...1
4'. xr/2-1=10,xr/2+1=12である。
10と15の最大公約数は5、12と15の最大公約数は3である。したがって、3と5は15の素因数である。
このアルゴリズムで最も時間がかかるのは、ステップ3のrを探すことである。従来のコンピュータは、ステップ3でrを探すのに時間がかかりすぎてしまう。そのため従来のコンピュータでは、はやく素因数分解を行うという点で、このアルゴリズムを使うメリットは薄かった。ところが、Shorは「離散フーリエ変換」を使って、量子コンピュータがrを一瞬にして見つけられることを示したのだ。これがShorの因数分解アルゴリズムの核心部分である。
Shorのアルゴリズムの概要
 |
ここではShorの因数分解アルゴリズムの概要を述べよう。先ほどの項目で紹介したように、因数分解を効率よく行うためには、上手に周期rを探すことが重要となる。
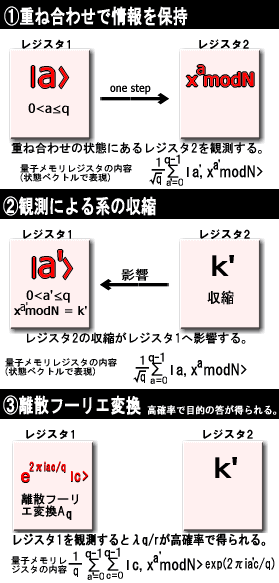
そこで、二つの量子メモリレジスタ(レジスタは一時的に情報を蓄えておく場所)を用意する(右図)。
①レジスタ1には、重ね合わせの状態で|a>(|
>は状態ベクトル表示)を蓄えておく(a=0,1,2,...,q-1,
n2<=q<2n2)。そしてこの重ね合わせの状態のまま、xamodNを計算する。このとき、従来のコンピュータならq回の処理を行なわなければならないが、量子コンピュータなら重ね合わせを利用して一括処理することが可能であることに注目しよう。この計算結果そのものも重ね合わせの状態でレジスタ2に蓄えられる。
②つぎにレジスタ2を観測する。観測する前は重ね合わせだったレジスタ2の状態は、ある値k'に収縮する。レジスタ2の収縮はレジスタ1にも影響する。しかし、注意しなければいけないのは、レジスタ1の|a'>はxa'modN=k'を満たしている限りは、収縮せずに、重ね合わせの状態を保っているということである。なぜならxa'modNは周期関数なので、例えば
xcmodN = xc+rmod = xc+2rmod = … =k'
とういように、a'がc,c+r,c+2r,...の重ね合わせの状態を保つことが出来るからだ。
③そして、レジスタ1の|a'>を離散フーリエ変換する。この変換を行うことで、レジスタ1の状態は右図のようになる。この変換後にレジスタ1を観測すると、量子力学的な干渉により、
λ(q/r)、λ=整数
という整数が高い確率で観測される。こうしてrを決定することができる。以上の①~③までの操作は、重ね合わせや確率的動作など、量子コンピュータにしかできないものだとされている。しかし、いったんrが決まれば、あとは従来のコンピュータでも、「なぜShorのアルゴリズムか?」の方法にしたがってステップ4で最小公倍数を求め、Nの因数分解を行うことが出来る。
以上に紹介したことはShorのアルゴリズムの大まかな流れであって、その詳細や離散フーリエ変換の性質などについては、下で紹介している文献を参考にするとよいだろう。
その他の量子アルゴリズム
ここでは詳しい内容に触れることはできないが、Shorのアルゴリズムの他にもGroverの検索アルゴリズムなどが有名である。N個のファイルのなかから特定のファイルを探し出す場合、古典的なコンピュータならおよそN/2程度のステップ数が必要なのに対し、GroverのアルゴリズムによるとN1/2ステップで高速に検索することができる。この差はファイル数Nが大きいときに明らかで、例えばN=1000のとき、古典的なコンピュータなら500ステップ数ほど必要なのに対し、量子コンピュータならたったの100ステップ程度ですむ。
また、量子スピン系や量子多体系の問題などについてのアルゴリズムも提案されている。
ref.
[1]P.W.Shor, Proceedings of the 35th Annual
Symposium on Foundations of Computer Science,
Santa Fe, NM, Nov. 20--22, 1994. /via xxx.lanl.gov
[2] L.K. Grover, Phys. Rev. Lett. 79 325, 1997
■数学的な予備知識 補足
[補足1]ユークリッドの互助法
ユークリッドの互助法とは、整数mとnの最大公約数を求める方法のことである(n>m)。nをmで割った余りをrとするとき、次のような操作を行なう。
1.r=0のとき、
mが最大公約数。
2.r≠1のとき、
(新しいn)=(これまでのm)
(新しいm)=(今の余りr)
とおき、計算を繰り返す。
例. n=1029, m=42のとき、最大公約数は21である。
| ステップ |
n |
m |
| 1 |
1029 |
42 |
| 2 |
42 |
21 |
| 3 |
21 |
0 |
[補足2]周期関数
xとNが互いに素であるとき(x<N)、
x0, x1, x2, x3,... ,xn, ...
という数列を用意したとき、それぞれのNの剰余
x0modN , x1modN, x2modN, ... , xnmodN, ...
は周期性をもった数列になることが知られている。このとき
x0modN = xrmodN = x2rmodN = ...
を満たす最小のrを、この関数の周期とする。
例.x=11, N=15のとき
| a |
xa |
xamodN |
| 0 |
1 |
1 |
| 1 |
11 |
11 |
| 2 |
121 |
1 |
| 3 |
1331 |
11 |
| ... |
|
|
よって、この場合の周期r=2である。
|
|
|