
 |
 |


|
最終更新日:2002/12/9



|
■自己組織化&自己集合
- 熱力学と自己組織化
前のページでは、自己組織化についていろいろな例を見てみた。しかし多様な現象例の一つ一つを眺めていても、自己組織化というものが何なのかは決して分からない。そこで熱力学的な立場から、自己組織化というものを整理してみることにしよう。
エントロピー増大の法則
自然と秩序が生じるという現象を議論しようとしたとき、あの有名な熱力学法則を思い出さずにはいられない人も少なくないだろう。そう、それは「熱力学の第二法則」、もっと一般的には「エントロピー増大の法則」などと呼ばれているものだ。エントロピーSというのは、大雑把にいえば乱雑さの指標のことだ。この法則によれば、エントロピーは増えつづける、つまり世界はよりランダムな方向へと向かうということになる。(式1)
d S/d t≧0 (孤立系) -(式1)
そうだとすると、自然と秩序化することは、この大原則と矛盾しているように思える。自然な秩序化はあり得ないことなのだろうか?多くの人にとって、すんなり自己組織化現象の概念を受け入れることが出来ない大きな原因はここにあるのではないだろうか。しかし実のところ、この法則が成り立つためには、いくつかの条件が仮定されていることに注目しなければならない。それは次のようなものだ。
1.孤立系
2.系を構成する粒子は理想気体分子
周囲とのあいだで、エネルギーや物質のやりとりをしない孤立系では、確かにエントロピーが増大しつづけ、いずれは熱力学的な平衡状態に達する。しかしこのような第二法則が成り立つ環境は非常に限られている。日常生活のほとんどは孤立系ではないし、分子も理想条件で振舞うとは限らない。すると、エントロピー増大が当てはまらないような場合が二通り考えられる。そのようなときに、自然な秩序化が現れてくるのだ。
まずしばらくの間は、この2通りの場合を「静的」な秩序化、「動的」な秩序化という直感的な分類によって考えてみることにしよう。そして後でその熱力学的な特徴に注目してみることにしよう。
「静的」な秩序化
飽和水溶液にタネを付けた糸を垂らしておけば自然とミョウバンの結晶は生成するし、脂質分子を水に混ぜておけば自然とミセルやニ分子膜などを形成する。これらは外部から遮断したビーカー内でも起こる現象で、確かに孤立系かつ平衡状態だといえる。しかし、結晶生成も脂質分子集合体も、分子間に化学結合や疎水結合などの相互作用がはたらいている。このように粒子間に強い相互作用がはたらいている場合は、第二法則だけでは実際に系がどのような傾向性をもっているかわからない。化学結合によるエネルギーの安定化も考慮に入れる必要がある。例えば、定温定圧の系では次の式を考慮に入れる必要がある。
⊿G = ⊿H - T⊿S - (式2)
ただしGはギブスエネルギー、Hはエンタルピー、Tは温度
この式2において、⊿G<0となるとき自発的な変化が起こる。したがって、ある変化でエントロピーが増大する(⊿S>0)のは一般的な傾向だが、そのときに系がエネルギー的に不安定になり(⊿H>0)、結果として⊿G>0となるのでは、その変化は自発的だとは考えられない。逆に⊿S>0でも、系がエネルギー的に安定化し(⊿H<0)、結果として⊿G<0となるなら、その変化は自発的だと考えられる。(下図を参照)
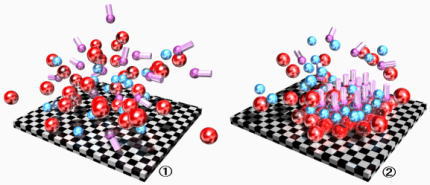
図.化学結合による系の安定化とエントロピー増大の綱引き
①から②への変化では明らかにエントロピーが減少する(⊿S<0)。しかし、化学結合によってエネルギー的に安定化する(⊿H<0)ことで、結果として⊿G<0となるのなら、この変化は自発的である。 |
そのため、粒子間にはたらく相互作用の種類が多様なほど、生じてくる秩序もより多様なものになるだろうと予想できる。とくに生体内では、共有結合(分子間で電子を共有することで生じる結合)意外にも、水素結合や配位結合、疎水結合などと、多様な分子間の相互作用にあふれている。様々な化学結合によって可能となるタンパク質の高次構造などがそのよい例である。とくに、DNAの二重らせん構造が提唱されて分子生物学が発展を遂げるなか、そういった知識が急速に蓄積されていった。
「動的」な秩序化
上で挙げた「静的」な秩序化はほとんどが平衡系の現象で、あくまで最終的な熱力学的安定性しか示されていない。しかし、秩序がうまれてくるのは必ずしも静的な場合だけとは限らない。一定のリズムをもった心臓の鼓動をはじめ、生物の営みそのものが動的(ダイナミック)なものだ。また、まわりの環境から遮断されたビーカーとも違って、呼吸や食べ物を摂取するというように外部とエネルギーや物質のやりとりを行っている。
このような場合、系のエントロピー変化については、式3のように表現できる。
d S/d t = d Si/d t + d Se/d t - (式3)
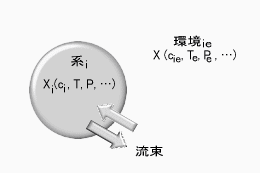
図.開放系の図式的な表示 |
ここでd Siは系内で起こる現象に基づくエントロピー生成、d Seは系とまわりの環境で流束の交換によるエントロピー変化、そしてd Sが結果としての系のエントロピー変化である。一般にd Si≧0が成り立っているが、系内のエントロピーをまわりの環境に放出すれば(d Se<0)、結果としてd S<0となることもありうる。つまり、開放系ではエントロピーを外部に放出することによって、系のエントロピーが減少することも起こるのだ。これが第二法則に対して、動的な秩序化が矛盾しない根拠となっている。
ただし今述べたことは、あくまで最終的なエントロピーの増減という静的な考察しかしていない。だが「動的」な秩序化を理解するためには、こういった静的な考察だけでなく、時間も含めた秩序化過程に注目する必要がある。この過程では、平衡からは程遠い非平衡になっており、またその数学的モデルは非線形なものとなっており非常に複雑な振る舞いを見せる。この「動的」な秩序化のダイナミクスについては、6章で詳しく述べることにしよう。
熱力学用語で整理すると…
さて、ここで「静的」とか「動的」といった直感的な言葉で説明してきた自然な秩序化を、熱力学のキーワードをいくつか用いることで整理してみよう。
表.「静的」、「動的」な秩序ア化とキーワードの関係
| |
特徴、キーワード |
「静的」な秩序化
⇒「自己集合」 |
平衡系
短距離的な相関 |
「動的」な秩序化
⇒「自己組織化」 |
非平衡系、開放系(散逸構造)
非線形の数学的モデル
長距離的な相関
空間パターンの出現 |
|
とくに注目すべきことは、「静的」な秩序化というのは局所的な化学結合が大きな原動力となっており、秩序化は短距離的な相関しか持っていない。例えば、化学結合の影響が及ぶ距離というのは数Åから遠くても数nm程度である。それに対し、「動的」な秩序化では空間全体に長距離的な相関が見られ、場合によっては巨視的なスケールでパターン形成が起こることもある。
さて、少し小うるさい定義の話になるが、ここら辺で「静的」、「動的」といった直感的な表現を改め、より厳密な用語に切りかえることにしよう。
非平衡での研究に大きな業績をあげ、新しい熱力学を切り開いていったノーベル化学者プリゴジン(I.Prigogine)は、とくに「動的」な秩序化が起こる非平衡開放系を「散逸系」とよび、散逸系での秩序形成を「自己組織化(self-organize,self-organization)」と定義した。一方、平衡系で起きる「静的」な秩序化のことを「自己集合(self-assemble,self-assembling)」と定義して、自己組織化と区別した。
これまでの文章では、曖昧に自己組織化という言葉を使ってきたが、今後のページではプリゴジンの定義に基づいて自己組織化、自己集合という言葉を使用していくことにしよう。3~5章では自己集合とナノテクとの関係を、6章では自己組織化とナノテクとの関係を、そして少々ナノテクからは脱線するが7章で自己組織化と複雑系との関係について見てみることにしよう。
|
|
 |